In Proposal of a "Quadratic Fit" Auto Focus evaluation method - Auto Focus - Main Sequence Software I suggested Quadratic Fit (QF) as an alternative method for the evaluation of best focus from Auto focus data. This is the base of Jerry’s application.
For the comparison of best focus results obtained from different evaluation methods an objective measure is needed to judge which one is superior. In the thread cited above, a simple method for this judgement was presented as well:
For both of the methods best focus vs. temperature (T) charts were plotted, a linear regression was made, and the temperature coefficient c (= negative slope of the fitting line) and the coefficient of determination, R^2, were calculated. The better method for evaluating best focus is the one which results in a better correlation of best focus with temperature, i.e. which results in the larger R^2.
In the course of our cooperation I developed a spreadsheet that is capable of processing the results of hundreds of AF runs at one blow. It calculates, displays and exports as graphic the quadratic fitting curve from the AF data of each AF run. Furthermore it displays the best focus vs. T plot for the whole data set, both for SGP’s and QF’s best focus results. The comparison of the best focus vs. T plots and the comparison of the calculated R^2 immediately shows which method is superior. The graphics Jerry presented are generated with this spreadsheet.
The underlying data were extracted from the SGP logfiles by Mikael’s (mikaelA) SGP AutoFocus LogViewer - Auto Focus - Main Sequence Software .
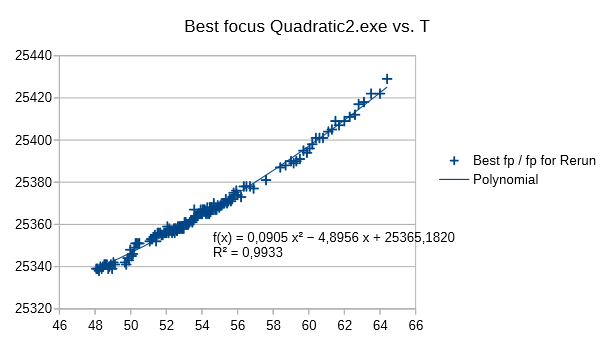
Actually the improvement of the best focus values that Jerry demonstrated above is such that a previously unvisible feature of his used instrument (Televue NP 127is) is revealed: the temperature coefficient is temperature dependent. At higher temperature, the temperature coefficient is larger than at lower temperature. This dependence is better described by a polynome of grade 2. Therefore I append one additional chart [3] that complements the charts presented by Jerry above:
[1] SGP: best focus vs. T, linear regression, R^2 = 0.9104, c = -5.2
[2] Quadratic: best focus vs. T, linear regression, R^2 = 0.9865, c = -5.2
[3] Quadratic: best focus vs. T, polynomial regression grade 2, R^2 = 0.9933, c: temperature dependent, see below
For case [3] the polynome is calculated as:
f(T) = 0.0905 T^2 - 4.90 T + 25365.2
The first derivative which gives the temperature coefficient then is:
f’(T) = 0.181 T - 4.90
(Important: T is specified in degrees F!)
This function must not be applied beyond the upper and lower bounds of the measured data, so the function is valid only in the temperature range from 48 to 64 degrees F. The change of the temperature coefficient is like this:
T [°F] c [steps/°F]
48 -3.8
50 -4.2
52 -4.5
54 -4.9
56 -5.2
58 -5.6
60 -6.0
62 -6.3
64 -6.7
I guess this is a convincing example for the superiority of QF to SGP’s current method.
Bernd